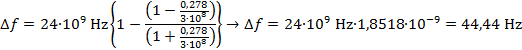Ergänzung zum eBook: Messen und Steuern mit dem Smartphone
Wie genau ist das Messergebnis? Bei der Durchführung erster Messungen wird wohl meist ein von der Seite geführter Schlag mit der flachen Hand ausgeführt, um ein Ergebnis zu erhalten. Schon bald stellt sich die Frage, wo es eine genaue Geschwindigkeitsreferenz in der Nähe gibt. Für die obige Handbewegung sind Messtabellen und Referenzwerte nicht verfügbar, soweit bekannt. Aus diesem Grund muss nach einem anderen Vergleich mit einer definierten Geschwindigkeit gesucht werden. Ein eigentlich nicht ganz so schwieriger Fall, da so naheliegend. Schon vor einiger Zeit haben sich Menschen mit diesem Problem beschäftigt, allerdings unter anderem Aspekt. Der Freie Fall aus der Klassischen Mechanik liefert hier die gewünschte Referenz. Es folgt ein Aufbau für Schreibtischtäter:
|
|||||||
|
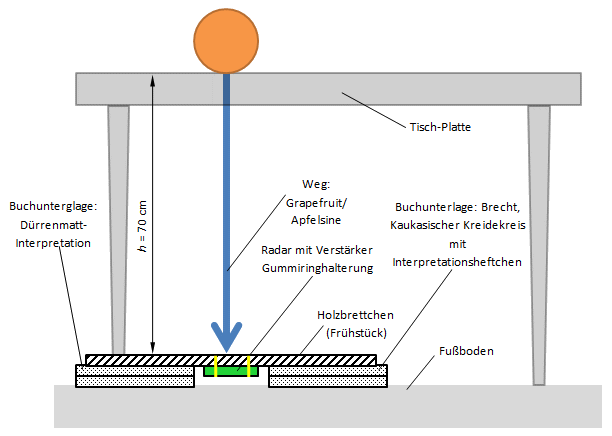
Versuchsaufbau für bequeme Schreibtischtäter |
|||||||
|
Eine Grapefruit fällt frei aus einer Höhe von 70 cm auf ein Holzbrett. Da Radar eine elektro-magnetische Welle im GHz-Bereich ist, stellt dünnes, trockenes Holz kein großes Hindernis dar. Der Sensor ist geschützt unter dem Brett mit zwei Gummiringen fixiert angebracht. Alle Körper fallen im Vakuum gleich schnell, heißt es. Es liegt hier zwar kein luftleerer Raum vor, trotzdem soll der Auftrieb und der Luftwiderstand der Frucht vernachlässigt werden können. Der Versuch könnte mit kleinen Eisen-, Blei- oder Stahlkugeln wiederholt werden... |
|||||||
|
Newton im Wohnzimmer Fall der Pampelmuse/Apfelsine/Grapefruit |
|||||||
|
Die Klassische Mechanik liefert die Formel der Geschwindigkeit beim 'Freien Fall':
Bei einer Fallhöhe h von 0,7 m und der mittleren Fallbeschleunigung g = 9,81 ms-2 berechnet sich die Geschwindigkeit zu:
Ausgehend von einem ganzzahligen Messergebnis können Werte zwischen 12 und 14 km/h noch im gültigen Bereich liegen. Hier könnte der Sketch umformuliert werden, um die Geschwindigkeit mit Nachkommastellen und in m/s an zu geben. |
|||||||
|
Durchführung |
|||||||
Die Einstellung der Verstärkung bzw. der Empfindlichkeit am Verstärker kann durch kurze Handbewegungen erfolgen. Die LED am Arduino leuchtet bei Messbereitschaft, also ohne Triggerauslösung. Das Potentiometer ist so einzustellen, dass im Ruhezustand noch gerade keine Messung ausgelöst wird. Nun kann die Anordnung positioniert werden und eine Probemessung erfolgen. Die Frucht wird entweder auf Höhe der Tischkante einfach losgelassen (ohne den Arduino zu treffen) oder sie wird über den Rand gerollt, so dass eine Art schiefer Wurf entsteht. Auch dabei ist die Fallzeit, sowie die Fallgeschwindigkeit trotz Parabelbahn laut Theorie ja gleich.
|
|||||||
|
Messergebnis Probemessung und relativer Fehler |
|||||||
|
Eine Grapefruit mit einem Durchmesser von etwa 8 cm liefert mehrfach reproduzierbar eine Anzeige von 12 km/h. Dem Reiz, auch hinter das Komma zu gucken, kann nicht widerstanden werden! Nach Änderung des Variablentyps für v und vmax in double und der Korrektur der Berechnungs- und Ausgabezeile v = (f*1e6)/44.0; // 24 GHz Radar Serial.print(vmax,2); Serial.println(" km/h");
Nach dem Fall der Kastanie aus eigener Feder - einem Video mit Einzelbild-Auswertung vor einer Steinmauer - bei dem die Zeit in Bild und der Weg in Stein gemessen wurde, sowie dem Fallversuch wie von Dr. Braak durchgeführt, bei dem mit Laptop und Soundsoftware die Zeit zwischen Schaltergeräusch und Aufprall akustisch bestimmt wird, nun also der Radarfall, bei dem die Messgröße direkt die Geschwindigkeit ist. |
|||||||
|
Verbesserter Trigger >1000fach besser |
|||||||
|
Als Verstärker ist ein Zweifach-Operationsverstärker verbaut, die einzelnen Stufen sind als invertierender Verstärker ausgelegt, wobei eine Stufe regelbar ist. Durch einen Spannungsteiler wird das Bezugspotenzial auf die halbe unipolare Betriebsspannung gelegt. Der Vorteil ist der Verzicht auf negatives Potenzial, der Nachteil scheint zunächst der für Digitaleingänge ungünstige Ruhepegel von 2,5 Volt zu sein. Wird ein Arduino (o.ä) eingesetzt, gilt diese Einschränkung nicht. Hat der Digitaleingang nur eine Schaltschwelle, so hat der Analogeingang mit 10-Bit-Auflösung 1024 Triggerschwellen. Aus diesem Grund wird nicht mehr digital, sondern analog ausgelöst. Wird nun der bisherige Digitaleingang (Pin 7) zusätzlich mit Analogeingang A0 verbunden, ist hoch auflgelöstes Triggern möglich, mit jeweils 512 Stufen oberhalb und unterhalb des Ruhepegels. Die Triggerschwelle ist im Sketch fest auf den Wert 30 eingestellt. Wird dieser Wert unterschritten, beginnt die Messfolge.
#define TRIGGER_IN A0 #define TRIGGER_LEVEL 30 #define RADAR_IN 7 #define RADAR_OUT 13 #define SCANS 8 int trigger; Der Deklarationsteil zeigt die Konstanten und eine Variable für den neuen Trigger. Der Ausgang Die Triggerung in der Hauptschleife sieht nun so aus: ... Serial.println("ready"); // Trigger; do {trigger=analogRead(TRIGGER_IN); analogWrite(RADAR_OUT, map(trigger, 0, 1023, 0, 255)); } while(trigger>TRIGGER_LEVEL); analogWrite(RADAR_OUT,0); ... Die Der Sketch für die Radarfalle - den Radarfall:
|
|||||||
|
Fazit |
|||||||
|
Eine Kalibrierung im Sinne der Definition des Sensors fand hier nicht statt. Vielmehr wurde mit einem bekannten Wert verglichen, also eine Art Referenzmessung durchgeführt. Ungenauigkeiten tauchen eher bei der Programmierung oder dem realen mechanischen Aufbau auf. Die Genauigkeit dieser Anordnung dürfte für viele Fälle hoch genug sein. Gab es beim Verkehrsradar nicht auch 10% Toleranz?
|
|||||||
|
Theoretischer Hintergrund Doppler-Frequenz |
|||||||
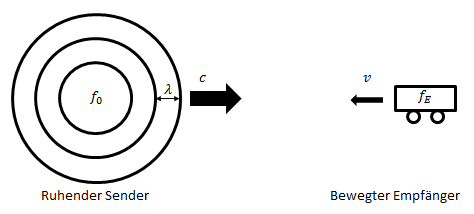
Zunächst der Fall, dass eine stehende Quelle (Sender) sein Signal mit der Sendefrequenz konzentrisch abstrahlt. Eine Welle bewegt sich dann mit der Geschwindigkeit c vom Sender weg in Richtung Empfänger. Der Empfänger bewegt sich mit der Geschwindigkeit v auf die Quelle zu. Die Wellenlänge bleibt konstant, es gibt also nur eine Änderung von Frequenz und Geschwindigkeit.
Entgegengesetzte Geschwindigkeiten addieren sich bei Annäherung zur Relativ-geschwindigkeit: Der Empfänger nimmt die erhöhte Empfangsfrequenz fE war, da pro Zeiteinheit mehr Wellen empfangen werden als bei Stillstand. Mit der Grundgleichung der Wellenlehre und deren verschiedenen Umstellungen
wird die Gleichung für die Empfangsfrequenz gefunden.
Nach dem Ausklammern der Sendefrequenz ergibt das:
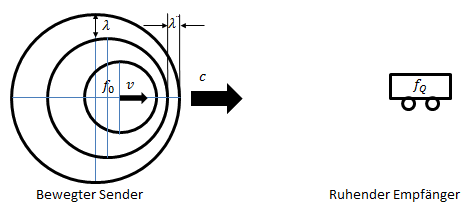
Dabei gilt (+) bei Annäherung und (-) bei Entfernung. Der umgekehrte Fall liegt vor, wenn die Quelle sich bewegt und der Empfänger ruht. Dann ist von außen betrachtet kein konzentrisches Wellenbild zu erkennen, da der Sender jeweils von einem anderen Ort sendet.
Die Wellenlänge verkürzt sich bei Annäherung zu lambda’. Während einer Schwingungsperiode T0 bewegt sich der Sender mit der Geschwindigkeit v um delta x:
Damit berechnet sich die veränderte Wellenlänge zu:
Für die Frequenz gilt dann Somit ist die Gleichung für die wahrgenommene Frequenz einer bewegten Quelle:
Dabei gilt (-) bei Annäherung und (+) bei Entfernung. Bei Radar-Messungen nach dem CW-Prinzip sendet der Sender ununterbrochen und empfängt eine Differenzfrequenz, auch Dopplerfrequenz genannt. Der ruhende Beobachter am Straßenrand sendet mit f0 und ein sich bewegender Gegenstand empfängt die veränderte Frequenz, die er reflektiert und als Frequenz fR ans bewegte Quelle ausstrahlt. Der ruhende Beobachter empfängt nun die Frequenz fQ, wobei die Sendefrequenz des bewegten Gegenstandes fR ist. Empfangsfrequenz des bewegten Gegenstandes: Empfangsfrequenz des ruhenden Beobachters: Die Differenz zwischen f0 und fQ bei Entfernung ist in diesem Fall also die Doppler-Frequenz:
Mit 24 GHz und 1 km/h bzw. 0,277 m/s berechnet sich die Doppler-Frequenz zu:
|
|||||||
Weitere Software
| Startseite | Bücher | Software | Digital RTV | Musik | Kontakt |
Für Inhalt und weitere Verzweigung externer Links sind die Betreiber der dortigen Seiten verantwortlich - H.-J. Berndt


 erscheint nun ein erster Messwert mit
erscheint nun ein erster Messwert mit